Resposta inelàstica
El mode d'expressió anterior [σ] en termes de [S] és vàlid per a sòlids que també mostren una resposta viscoelàstica o plàstica, tret que [S] només s'ha de considerar només com a funció del present [E M] i θ, però també depenen de la història prèvia d’ambdues. Si suposem que aquests materials mostren resposta elàstica a canvis sobtats de tensió o a petites descàrregues d’un estat deformant plàsticament, [S] encara es pot expressar com a derivat de f, com anteriorment, però s’entén que el derivat es fa respecte a un elàstic. variació de la soca i s'ha de prendre a fixed fixa i amb deformació inelàstica prèvia i antecedents de la temperatura. Aquesta dependència de la història de vegades es representa com una dependència de f de variables d'estat intern les lleis de l'evolució formen part de la descripció constitutiva inelàstica. També hi ha models més senzills de resposta inelàstica. A continuació, es presenten les formes més freqüents de plasticitat i fluïdesa en sòlids isotròpics.
A bona aproximació, la deformació plàstica de sòlids cristal·lins no provoca cap canvi de volum; i els canvis hidrostàtics d’estrès, que suposen un canvi igual de totes les tensions normals, no tenen cap efecte sobre el flux de plàstic, almenys en canvis que siguin del mateix ordre o magnitud que la força del sòlid en la cisalla. Així, la resposta plàstica sol formular-se en termes d’estrès deviatòric, que es defineix per τ ij = σ ij - δ ij (σ 11 + σ 22 + σ 33) / 3. Després de Richard von Mises, en un procediment que es troba d’acord moderadament bé amb l’experiment, la relació de flux plàstic es formula en termes del segon invariant de l’estrès deviatòric, normalment reescrit com
i es deia tensió de tracció equivalent. La definició es fa de manera que, per a un estat de tensió uniaxial, σ sigui igual a l'estrès de tracció i la relació estrès-tensió per als estats de tensió general es formuli en termes de dades de la prova de tracció. En concret, una soca de plàstic ε p en un test de tensió uniaxial es defineix a partir de ε p = ε - σ / E, on ε s'interpreta com la soca en la prova de tracció segons la definició logarítmica ε = lnλ, el mòdul elàstic E és Se suposa que no es va modificar amb la deformació, i σ / E << 1.
Així, en la versió de la teoria de la plasticitat independent de la taxa, es suposa que les dades de tracció (o compressives, amb reversions de signes adequades) d'un test de càrrega monotònica defineixen una funció ε p (σ). A la versió viscoplàstica o a alta temperatura de fluix de la teoria, les dades de tracció s’interpreten per definir dε P / dt com a funció de σin el cas més simple, representant, per exemple, el creep secundari, i com a funció de σand ε p en les teories. destinada a representar efectes de transmetre transitoris o resposta sensible al ritme a temperatures més baixes. Considereu primer el model de material rígid-plàstic en què s’ignora la deformació elàstica del tot, com a vegades és apropiat per a problemes amb un gran flux plàstic, com en la forma de metalls o un trencament a llarg termini al mantell de la Terra o per a l’anàlisi de les càrregues de col·lapse plàstic en les estructures. La velocitat de deformació del tensor D ij està definida per 2D ij = ∂v i / ∂x j + ∂v j / ∂x i, i en el cas rígid-plàstic [D] es pot equiparar al que es pot considerar la seva part plàstica. [D p], donat com D p / ij = 3 (dε p / dt) τ ij / 2σ. Els factors numèrics asseguren un acord entre D p / 11 i d p / dt per a tensió uniaxial a la 1direcció. A més, l’equació implica que
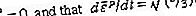
que s’ha d’integrar a la història anterior per obtenir ε p segons es requereix per als models viscoplàstics en els quals dε p / dt és funció de σ i ε p. A la versió independent de la tarifa, [D p] es defineix com a zero sempre que σ sigui inferior al valor més alt que ha assolit a la història anterior o quan el valor actual de σ és el valor més alt, però dσ / dt <0. (En el context elàstic-plàstic, això vol dir que la "descàrrega" només comporta una resposta elàstica.) Per al sòlid idealment plàstic, idealitzat per poder fluir sense augment d'estrès quan σ és igual al nivell de força de rendiment, dε p / dt és es considera un paràmetre no determinat, però necessàriament no negatiu, que només es pot determinar (de vegades no de manera exclusiva) només mitjançant la solució completa d'un problema de valor de frontera de la mecànica sòlida.
El model de material elàstic-plàstic es formula llavors escrivint D ij = D e / ij + D p / ij, on D p / ij es dóna en termes d’estrès i possiblement de velocitat d’esforç com anterior i on les taxes de deformació elàstica [D e] estan relacionats amb les tensions mitjançant l'expressió elàstica lineal habitual D e / ij = (1 + ν) σ ij * / E - νδ ij (σ 11 * + σ 22 * + σ 33 *) / E. Aquí els índexs d’estrès s’expressen com els índexs de co-rotació de Jaumann

és un derivat seguint el moviment d’un punt material i on el gir Ω ij es defineix per 2Ω ij = ∂v i / ∂x j - ∂v j / ∂x i. Els índexs de tensió co-rotacionals són els calculats per un observador que gira amb la velocitat angular mitjana d’un element material. La part elàstica de la relació tensió-tensió hauria de ser coherent amb l’existència d’una energia lliure f, com s’ha comentat anteriorment. Aquesta forma no s’aconsegueix estrictament amb la forma que s’acaba de donar, però les diferències entre aquesta i una que és coherent d’aquesta manera comporten termes addicionals que són de l’ordre de σ / E 2 vegades més que σ kl * i són insignificants en casos típics en què la teoria s’utilitza, ja que σ / E sol ser una fracció extremadament petita d’unitat, per exemple, de 10 −4 a 10 −2. Una versió petita de la teoria de la teoria és d'ús comú per a anàlisis de tensió elàstica-plàstica. En aquests casos, [D] es substitueix per ∂ [ε (X, t)] / ∂t, on [ε] és el tensor de tensió petita, ∂ / ∂x amb ∂ / ∂X en totes les equacions, i [σ *] amb ∂ [σ (X, t)] / ∂t. Els dos darrers passos no sempre es poden justificar, fins i tot en casos de tensió molt petita quan, per exemple, en un material independent de la velocitat, dσ / dε p no és gran en comparació amb σ o quan les taxes de rotació de fibres materials poden ser molt més grans. que les taxes d’estirament, cosa que preocupa problemes problemàtics fins i tot en sòlids purament elàstics.