Hipòcrates de Chios (fl. C. 460 aC) va demostrar que les zones en forma de lluna entre els arcs circulars, conegudes com a lunes, es podien expressar exactament com una zona rectilínia o quadratura. En el cas senzill següent, dues lunes desenvolupades al voltant dels costats d'un triangle dret tenen una àrea combinada igual a la del triangle.
-
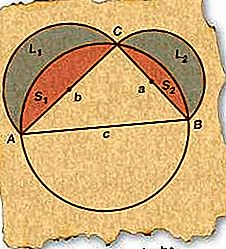
A partir de la dreta ΔABC, dibuixa un cercle el diàmetre del qual coincideix amb AB (costat c), la hipotenusa. Com que qualsevol triangle dret dibuixat amb un diàmetre d’un cercle per a la seva hipotenusa s’ha d’inscriure dins del cercle, C ha d’estar al cercle.
-
Dibuixeu semicercles amb els diàmetres AC (costat b) i BC (costat a) com a la figura.
-
Etiqueta les llunes resultants L 1 i L 2 i els segments S 1 i S 2 resultants, tal com s’indica a la figura.
-
Ara la suma de les llunes (L 1 i L 2) ha de ser igual a la suma dels semicercles (L 1 + S 1 i L 2 + S 2) que els conté menys els dos segments (S 1 i S 2). Així, L 1 + L 2 = π / 2 (b / 2) 2 - S 1 + π / 2 (a / 2) 2 - S 2 (ja que l’àrea d’un cercle és π vegades el quadrat del radi).
-
La suma dels segments (S 1 i S 2) és igual a l’àrea del semicercle basada en AB menys l’àrea del triangle. Així, S 1 + S 2 = π / 2 (c / 2) 2 - ΔABC.
-
Substituint l’expressió al pas 5 al pas 4 i desglossant els termes comuns, L 1 + L 2 = π / 8 (a 2 + b 2 - c 2) + ΔABC.
-
Com que ∠ACB = 90 °, a 2 + b 2 - c 2 = 0, pel teorema de Pitàgores. Així, L 1 + L 2 = ΔABC.
Hipòcrates va aconseguir quadrar diversos tipus de llunes, algunes sobre arcs més grans i inferiors als semicercles, i va entendre, encara que potser no ho cregués, que el seu mètode podia quadrar un cercle sencer. Al final de l'edat clàssica, Boethius (c. Ad 470–524), les traduccions llatines dels fragments d'Euclides mantindrien la llum de la geometria parpellejant durant mig mil·lenni, va mencionar que algú havia aconseguit la quadratura del cercle. Si el geni desconegut va utilitzar lunes o algun altre mètode no es coneix, ja que per falta d'espai Boethius no va donar la demostració. Així, va transmetre el repte de la quadratura del cercle juntament amb fragments de geometria aparentment útils per realitzar-lo. Els europeus van mantenir la tasca desgraciada fins a la Il·lustració. Finalment, el 1775, l'Acadèmia de Ciències de París, farta de la tasca de descobrir les fal·làcies en les nombroses solucions que se li van presentar, va negar-se a res més a veure amb els quadrats.













